Amateurfunk DL1JWD

Spulenrechner

Schaltungsberechnungen oder mathematische Simulationen geraten schnell in Widerspruch zur Realität, wenn Verluste und parasitäre Effekte der Bauelemente unberücksichtigt bleiben.
Besonders augenfällig wird dies bei Induktivitäten, weil deren Wicklungskapazitäten und der Skineffekt mit zunehmender Frequenz zunehmend an Einfluss gewinnen.
Deshalb grübelt mancher OM, warum denn eine von ihm sorgfältig berechnete HF-Drossel auf den oberen Bändern ihre Sperrwirkung vollständig verliert oder warum denn seine selbstgewickelte Luftspule sich plötzlich wie eine Kapazität verhält.
Gemäß dem Prinzip "soviel wie nötig" liefert das Tool den Frequenzgang einer Induktivität auf Basis eines vereinfachten Ersatzschaltbildes (es wird nur die erste Parallelresonanz berücksichtigt).
Das gleiche mathematische Modell findet auch im KNWA-Tool und in HamVNAS Verwendung.

Dem SR müssen lediglich vier Werte von L vorab bekannt sein: Die Frequenzskala ist logarithmisch geteilt, wobei zwei Bereiche zur Auswahl stehen:

Wichtig:

Wesentlicher Unterschied der aktuellen V1.1 des Spulen-rechners zum Vorgänger ist die komplett überarbeitete Info-Datei. Diese enthält jetzt auch Beispiele zur Güte-bestimmung auf Basis von Messungen mit dem NanoVNA (Software nanovna-saver).

Beispiel 1:
Fastron-SMCC-Drossel 47uH

Für ein Selbstbauprojekt wie beispielsweise einen "Breitbandverstärker für aktive KW-Empfangsantenne" benötigt man HF-Drosseln.
Diese müssen i.d.R. eine gegenüber 50Ohm hohe Sperr­impedanz haben.
Geeignet für diese Aufgabe scheint z.B. die bekannte Fastron-SMCC-Drossel 47µH zu sein, wie sie auch im NORTON-Verstärker der QRP-AG zum Einsatz kommt.

Wie groß sind Scheinwiderstand und Sperrdämpfung dieser Drossel auf den klassischen Amateurfunkbändern?

Zunächst füttern Sie den SR mit den im Datenblatt preisgegebenen Werten für die Induktivität (47µH) und für die Resonanz­frequenz Fo (7,5MHz).
Der Wert für die Parallelkapazität (9,58pF) wird automatisch ergänzt. Genausogut könnte man aber auch zuerst Cp eingeben (falls bekannt) und sich dann Fo ausrechnen lassen.
Den Gleichstromwiderstand der Wicklung (0,1Ohm) kann man messen oder auch schätzen, seine genaue Größe ist, zumindest für unsere Einsatzszenarien, bedeutungslos.
Alle Eingaben sind mit der ENTER-Taste abzuschließen (die gelb gefärbten Felder weisen darauf hin).

Aber woher den Gütefaktor QL nehmen?
Wir versuchen es zunächst mit dem für Drosseln typischen Wert QL = 10.

Für die Sperrdämpfung TL(dB) bei Resonanz hat der SR bereits automatisch den von QL abhängigen Wert (46,94dB) berechnet und eingetragen.

Nach Klick auf den "START"-Button erscheint der Übertragungsfrequenzgang, wobei sofort das Dämpfungsmaximum von 47dB bei 7,5MHz ins Auge springt.
Mit der Maus kann man jetzt das Frequenzlineal im unteren Diagramm hin- und herbewegen,
wobei die laufenden Werte für Frequenz, Sperrdämpfung und Impedanz angezeigt werden:

Beispiel 1

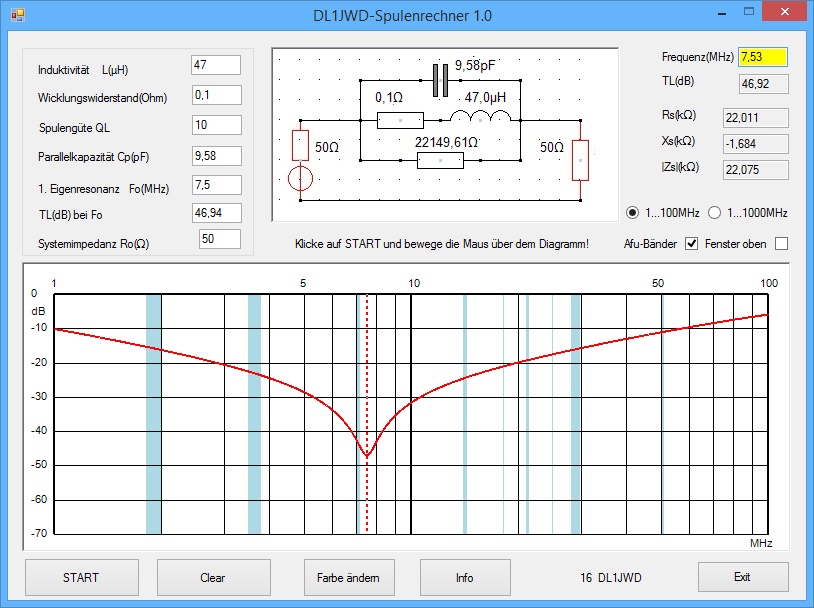
Oberhalb der Resonanzfrequenz wechselt das Vorzeichen von Xs, die Spule wirkt nur noch als verlust­behaftete Kapazität und die Sperrdämpfung geht mit weiter wachsender Frequenz immer mehr verloren.

Beispiel 2:
Neosid SDS-Drossel 47uH

Die 47µH-Fastron-SMCC-Drossel konnte mich aufgrund ihrer niedrigen Parallelresonanz, die in unmittelbarer Nähe des 40m-Bands liegt, und ihrer ungenügenden Sperdämpfung nicht überzeugen.
Außerdem zeigen VNA-Messungen knapp oberhalb 30MHz bereits eine unangenehme Serienresonanz.
Bei Ebay stieß ich durch Zufall auf die 47µH-Neosid SDS-Drossel, mit einer garantierten Parallelresonanz von mindestens 12MHz und einem Stückpreis von nur 10Cent.

Beispiel 2
Die Güte QL wollte ich aber diesmal nicht schätzen, sondern vorab durch eine Messung mit dem VNA genauer bestimmen.

Wie kann man die Spulengüte mit dem VNA messen?

Zwar ist QL frequenzabhängig, aber interessant ist hier nur die Spulengüte bei der Resonanz­frequenz.
Mein miniVNApro "wobbelt" für die 47µH-Neosid-Drossel im Transition-Mode den folgenden Dämpfungsverlauf im Bereich von 1... 50MHz:

Beispiel 2
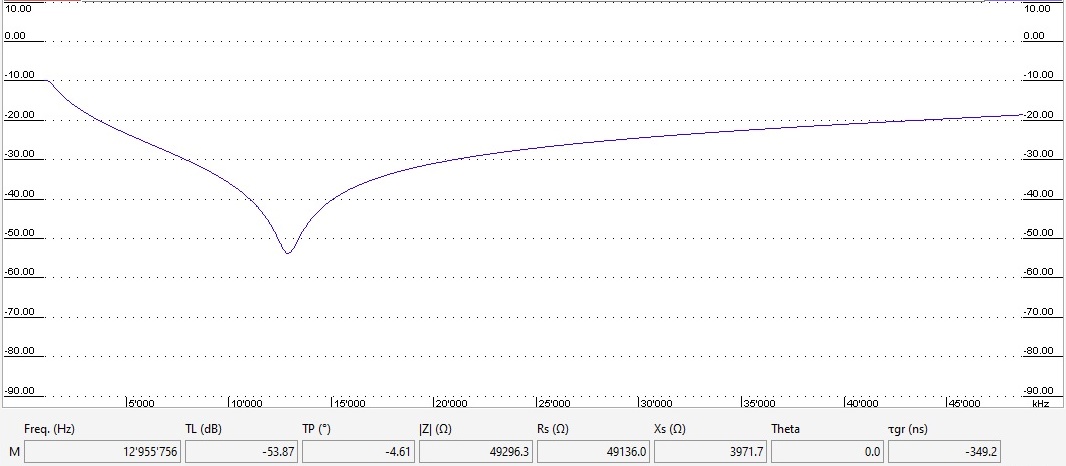
Aus dem Diagramm lässt sich eine Resonanzfrequenz von 13MHz ablesen, an dieser Stelle beträgt die Durchgangsdämpfung TL ca. 54dB.
Beide Werte gebe ich in den SR ein, die Spulengüte QL=13 wird automatisch ergänzt.
Der SR erzeugt nach Klick auf"START" ein fast identisches Diagramm:

Beispiel 2
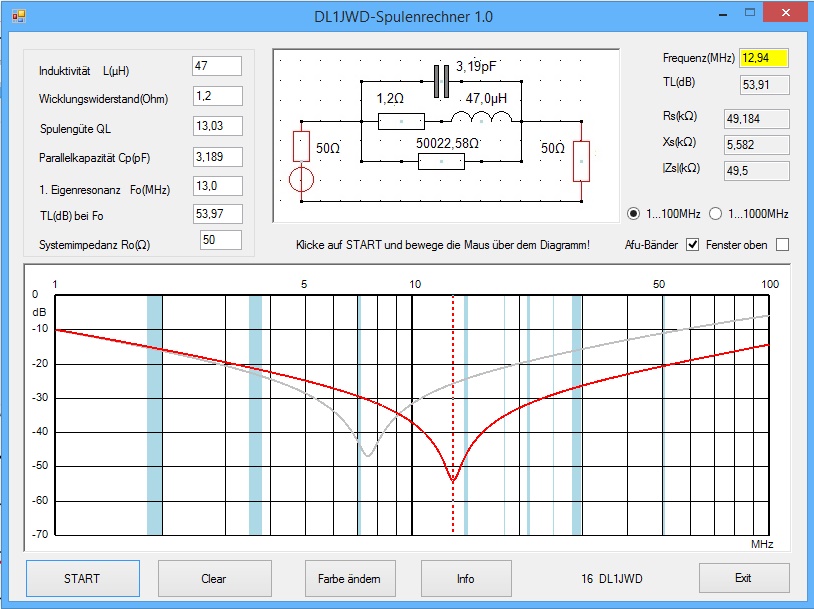
Im abgebildeten Diagramm ist auch noch die Kurve der Fastron-Drossel in grauer Farbe hinterlegt.
Man erkennt die deutliche Überlegenheit der Neosid-Drossel.

Beispiel 3:
Mantelwellensperre

Zur Unterdrückung von Mantelwellen und Störeinstrahlungen habe ich, wie allgemein üblich, in mein (stehwellenfreies) 50Ohm-Antennenkabel einen 1:1-Strombalun eingeschleift.

Dieser besteht aus 24Wdg dünnem Koaxkabel RG316U, die ich auf den größten in der Bastelkiste auffindbaren Ferrit-Ringkern (AD=56mm, ID=35mm, H=12mm) gewickelt habe.
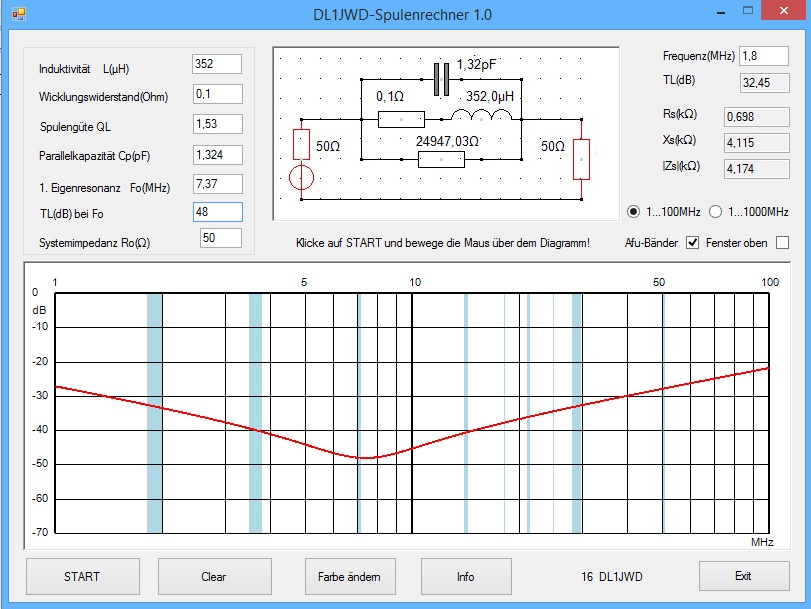
Die niederfrequente Induktivitätsmessung ergibt 352µH, der Gleichstromwiderstand ist geringer als 0,1Ohm.

Beispiel 3 Mit dem miniVNA messe ich die erste Parallelresonanz bei 7,37MHz, die entsprechende Durchgangsdämpfung beträgt 48dB.

Der SR bestätigt den gemessenen Dämpfungsverlauf (Abweichungen kleiner 10%) und zeigt, dass im KW-Bereich (1,8...30MHz) ein akzeptabler Wert von besser 30dB erreicht wird:
Beispiel 3